word2vec skip gram model 公式推导
2018-07-15
skip gram model
skip gram 模型简单的来说就是用语料集中的一个词语来预测其周围的词语。其输入时一个词语$W_I$,假设窗口宽度为C,输出是$W_I$的上下文${W_{O,1},W_{O,2},…,W_{O,C}}$。比如”我/爱/自然语言处理/和/机器学习”这句话,如果让”自然语言处理”是输入词,那么输出就是{“我”,”爱”,”和”,”机器学习”}。神经网络当然不能直接处理单词,我们用长度为$V$的one-hot向量表示每一个单词,其中$V$是预料集中所有不同的单词数。one-hot向量对应于单词$W_I$的位置是1,其他元素都是0。我们可以从语料集中收集到大量的训练样本。
Forward Propagation
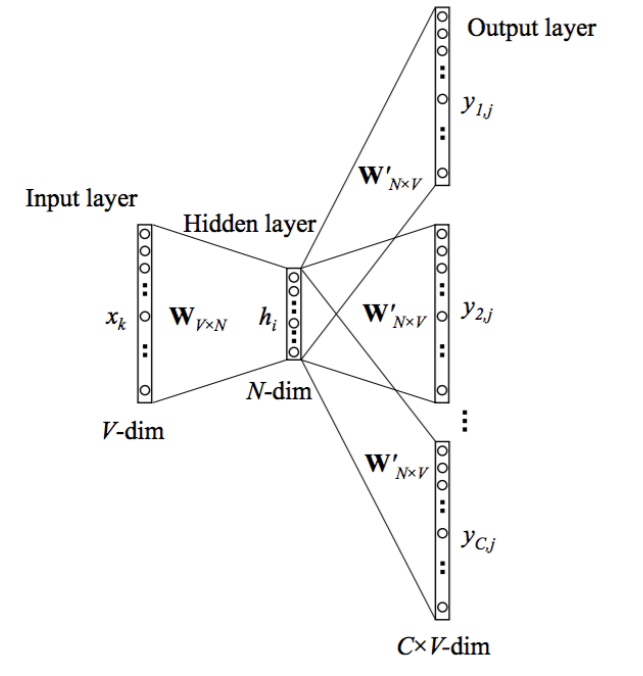
skip-gram 模型的神经网络结构如上图所示。我们需要注意几个符号的表示:
- $x$是代表输入的one-hot向量。对应于输入的单词。其大小是$V\times1$,$V$是整个词表的大小。
- ${y_1, …, y_C}$代表输出的one-hot向量。对应于输出的单词,也就是输入单词的上下文。
- 网络中只有一个隐藏层,其节点数是$N$。最后我们得到的词向量也是$N$。
- $W$是输入层到隐藏层之间的权重矩阵,大小是$V \times N$。由于输入是个one-hot向量,故单词$W_k$的向量和$W$的乘积就是$W$的第k行,因此可以把$W$看出是一个词向量表。$W$也是我们整个模型关注的重点。
- $W^\prime$是隐藏层到输出层之间的权重矩阵。是一个$N\times V$的矩阵。
- $h$是隐藏层的输入, 是输入向量和权重矩阵的乘积。由于输入向量只有一个位置$k$是1,因此$h$就是输入到隐藏层的权重矩阵$W$的第$k$行。 其中$v_{w_k}$表示权重矩阵$W$的第$k$行向量。
- 由于隐藏层没有激活函数,所有$h$也是隐藏层的输出。
- $u_c$是第c个输出单词的输入。$u_c$是一个$V\times1$的向量。 值得注意的是skip_gram模型共有$C$个需要预测的单词,可以把输出层看做是有$C\times V$个节点。但是每个预测单词都共享权重矩阵$W^\prime$,因此所有的$u_c$都是相同的。
第$c$个输出词的第$j$个节点的输入就是$u_c$的第$j$个元素。
其中$v^{\prime T}_{w_j}$是$W^\prime$的第j列。
- 第$c$个输出词的第$j$个节点的输出通过
softmax函数计算,softmax函数产生一个多项式分布。
$y_{c,j}$是在输入词是$w_I$的条件下,第$c$个输出词是词表中第$j$个词的概率。我们的训练目标就是要$y_{c,j}$等于真实的第$c$个输出词的第j个节点的值。输出是one-hot变化,我们知道真实的$y_{c,j}=1$,如果第$c$个输出词是词表中第$j$个词的话,否则是0。
Learning the Weights with Backpropagation and Stochastic Fradient Desecent 用后向传播和随机梯度下降学习权重矩阵
上面的这个过程就是输入以前向传播的方式经过神经网络产生输出的过程。最初网络中的两个权重矩阵$W$和$W^\prime$是随机初始化的,我们可以通过后向传播和随机梯度下降方法学习这两个权重矩阵。
定义loss function
损失函数就是给定了输入词后输出词的条件概率的负对数。其中$j_c^*$是第$c$个输出词在词表中索引。我们的目标就是使条件概率的负对数最小。
推导输出层权重矩阵$W^\prime$的更新公式
先来推导一下隐藏层-输出层的权重矩阵$W^\prime$的更新公式。首先计算一下损失函数$E$对$u_{c,j}$的偏微分。根据链式法则:
先来看偏微分的第一项,只有当$j_c^*$和$(c,j)$相同时,才为1,否则为0。我们用$t_{c,j}$表示这一项的微分,即,当第c个输出词的第j个节点的真实值是1,$t_{c,j}=1$,否则$t_{c,j}=0$。
偏微分的第二项可以用链式法则求解:
我们可以看到偏微分的第二项刚好就是第c个输出词第j个节点的输出$y_{c,j}$。因此:
现在我们有了最后一层节点输入的误差导数,接下来我们继续用链式法则来纠结损失函数关于输出权重矩阵$W^\prime$的偏微分。
回想一下
因此:
所以:
根据随机梯度下降算法,输出层权重矩阵$W^\prime$的更新公式为:
其中 $\eta>0$ 是学习率。
推导输入层权重矩阵$W$的更新公式
继续使用链式face推导隐藏层权重矩阵$W$的更新公式:
最后隐藏层权重更新矩阵:
由此可以看出,每更新一个参数都需要对整个词表求和,计算量很大。Word2Vec的作者也此做了一些优化,如hierrachical softmax 和 负采样(negative sampling)。
阅读全文 »
Word2Vec
2018-07-13
word2vec的两种模型:
- CBOW
- skip gram
skip gram 模型的结构:
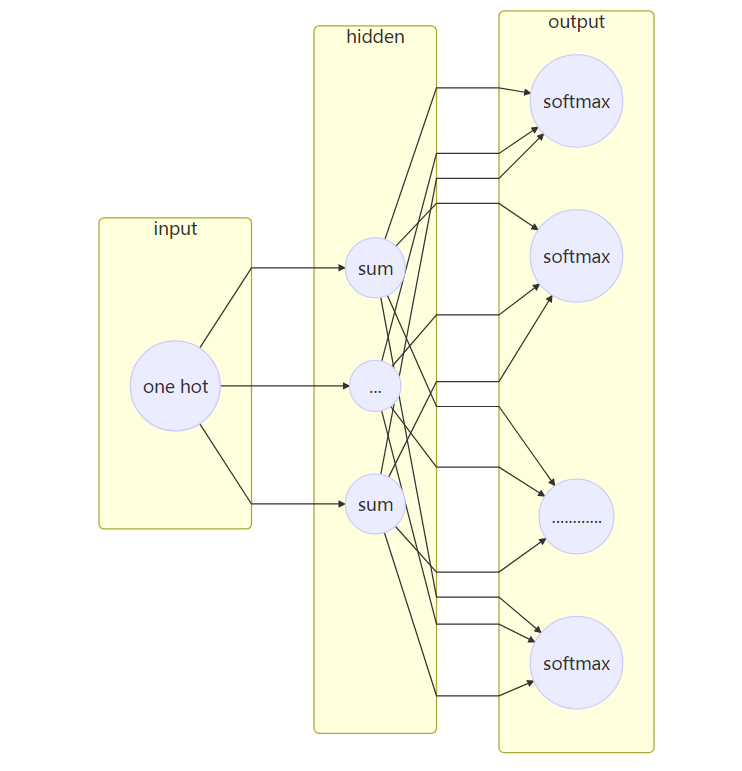 参数数目: 2 * d * V
其中d是隐藏层的数目也是最后输出的词向量的维数。V是词典的大小,也就是语料集中共有V个不同的词。输入层到隐藏层的权重矩阵U是一个V*d的矩阵。由于输入是一个one-hot向量, 输入向量x隐藏层矩阵的乘积$XU$(假设x是第t个词)刚好是U的第t行,因此可以把矩阵U看做是一个
参数数目: 2 * d * V
其中d是隐藏层的数目也是最后输出的词向量的维数。V是词典的大小,也就是语料集中共有V个不同的词。输入层到隐藏层的权重矩阵U是一个V*d的矩阵。由于输入是一个one-hot向量, 输入向量x隐藏层矩阵的乘积$XU$(假设x是第t个词)刚好是U的第t行,因此可以把矩阵U看做是一个lookup table。而隐藏层到输出层的矩阵是中心词的上下文矩阵。
求解方式的优化:
- negative sampling
- Hierarchical softmax
negative sampling
- Treating common word pairs or phrases as single “words” in the model, 把经常出现在一起的短语看做一个词
- Subsampling frequent words to decrease the number of training examples, 对高频词进行下采样,减少训练样本的数目
- Modifying the optimization objective with a thechniuqe they called “Negative Sampling”, which causes each training sample to update only a small percentage of the model’s weights. 用
负采样的技术减少每个训练样本更新的参数数目。
Word Pairs and “Phrases”
把常见的搭配和短语看做一个词,减少词汇总数。
Subsampling Frequent Word
word2vec是一个具有一层的神经网络。输入向量是语料中的每个词,训练目标是这个词周围的词。周围的词是只一个窗口内的词,比如window=5就是中心词t前的5个词和后面的一个词。下图是以window=2为例,展示了word2vec训练样本的生成过程。

对于像”the”这样的高频词,有两个问题:
- 词语对(”for”, “the”)并不能告诉我们”fox”的意义,”the”在许多词语的上下文环境中都会出现。
- 包含有”the”的词语对(“the”,…)很多,而学习一个好的向量表示”the”并不需要很多词语对。
Wprd2Vec用下采样来解决上面的两个问题。对于训练集中的每个词,都有一定的概率把它从文本中删掉,删掉的概率和词频有关。
假如窗口的长度是10,把某个词(比如‘the’)移除之后,会有下面两个效果:
- 当我们训练剩下的词的,并不是所有的词都要和“the”配对。
- 当“the”是中心词的时候,我们的训练样本会少于10个。
这样就可以解决了上面说的两个问题。
Sampling rate
在Word2vec 的C代码中,有个公式决定了一个词被保留在语料中的概率。 假设$w_i$是词,$z(w_i)$是词$w_i$在语料中出现的次数和语料中所有词的总次数的比值。例如,单词“peanut”出现了1000次,预料中总次数是100000000,那么$z(‘peanut’)=1E-6$。
在代码中,有个变量是sample决定了下采样的比率,sample的默认值是0.001。sample的值越小,说明词被删掉的概率越大。
一个词被保留的概率$P(w_i)$用如下方式计算:
用Python把这个式子画出来,可以看到,当$z(w_i)$很小时,$P(w_i)$比较大,而当$z(w_i)$很大时,$P(w_i)$很小。
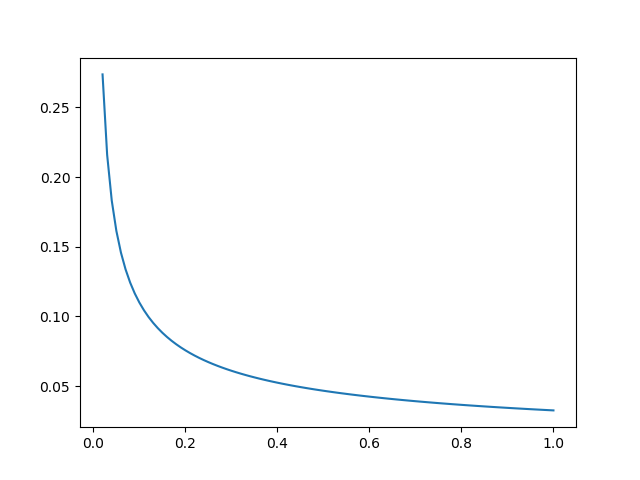
- 当$z(w_i)<=0.026$时,$P(w_i)=1.0$,也就是说,只有词语出现的频率大于0.26%时才会被下采样
- 当$z(w_i)=0.00746$时,$P(w_i)=0.5$,一半的词会被保留。
- 当$z(w_i)=1$时,$P(w_i)=0.033$,也就是说当整个语料集只有一个词时,只有3.3%的机会会被保留。但这样的语料当然是很荒谬了。
负采样 Negative Sampling
训练一个神经网络意味着,当一个训练集喂给网络时,我们对所有神经元的权重做微调,使网络对这个样本的预测更加准确。也就是说,每个训练集都会改变神经网络中的所有权重。
前面我们算过,word2vec中的参数的数目跟词典数目成正比。一般一个语料集中的词语数目都是几十万甚至上百万,这也意味着神经网络中巨大的参数数目。Word2vec中训练集的数目通常会更多,有可能到上亿词。如果每次都调整所有神经元的权重,计算量将非常大。
为了减少计算量,负采样每次只更新小部分参数,而让大部分参数保持不变。当训练样本是(“fox”,”quick”)时,神经网络的输出是一个ont-hot向量,只有对应于”quick”的神经元应该输出1,其他神经元都是0。当进行负采样时,我们随机选择数目很小的一些负词进行权重的更新。在这里负词是指神经元的期望输出是0的词。同时,正词(在这个例子里就是”quick”)的权重也会被更新。这里所说的更新都是隐藏层到输出层的权重。
论文表明对于小的数据集,5-20个词表现会很好,大的数据集只需要更新2-5个词。
假设我们词表的数目是10000,隐藏的节点数是300, 那么整个网络的参数是200*10000。但使用负采样每次训练只需要更新正词(“quick”)和其他的5个负词。也就是6个神经元,1800个参数。无论使用负采样与否,输入层到隐藏层的参数都是只更新中心词的参数。
Selecting Negative Samples
负词的采用是根据unigram distribution(一元语言模型)进行的。本质上来说,选择一个词做负词的概率和这个词的频率有关,高频词被选中的概率越高。
在word2vec中,这个概率的计算方式如下:
论文中,根据实验决定用3/4次方而不是频率本身。
在C代码中,负采样的实现也很有意思。他们用了一个有100M元素的数组代表unigram 词表。数组中的元素是词在词表中的索引。每个索引出现的次数等于$P(w_i)*table_size$。当进行一次负采样时,只要生成一个在0到100M之间的随机数,数组在这个位置的词就是所谓的负词。概率越大的词的索引在数组中出现的次数越多,因此,被采集到的机会也越大。
参考: word2vec-tutorial-part-2-negative-sampling 作者还对谷歌开源的C代码做了注释,有时间可以看一下。
http://mccormickml.com/assets/word2vec/Alex_Minnaar_Word2Vec_Tutorial_Part_I_The_Skip-Gram_Model.pdf
http://mccormickml.com/assets/word2vec/Alex_Minnaar_Word2Vec_Tutorial_Part_II_The_Continuous_Bag-of-Words_Model.pdf
阅读全文 »
pyspark 使用udf遇到的问题
2018-02-24
在使用PySpark的DataFrame处理数据时,会遇到需要用自定义函数(user defined function, udf)对某一列或几列进行运算,生成新列的情况。PySpark的udf使用方法如下。
先初始化SparkContext和SparkSession
from pyspark import SparkConf
from pyspark import SparkContext
from pyspark.sql import SparkSession
spark_conf = SparkConf().setAppName("udf_example")
spark_context = SparkContext(conf=spark_conf)
spark = SparkSession.builder.config(conf=spark_conf).enableHiveSupport().getOrCreate()
使用装饰器的方法把一个python函数注册为udf
from pyspark.sql.types import IntegerType
from pyspark.sql.functions import udf
# 使用装饰器把一个python函数注册为udf, 装饰器中的参数为返回的数据类型
@udf('int')
def slen(s):
if s is not None:
return len(s)
# 当装饰器不带任何参数时,默认的数据类型为str
@udf()
def to_upper(s):
if s is not None:
return s.upper()
# 也可以使用pyspark.sql.types作为装饰器的参数指定udf返回类型
@udf(IntegerType())
def add_one(x):
if x is not None:
return x + 1
# 也可以先定义一个python函数,然后用udf注册
def add_two(x):
if x is not None:
return x + 2
add_tow_udf = udf(add_two, IntegerType())
# 创建一个DataFrame
df = spark.createDataFrame([(1, None, 21), (2, 'Lucy', 20)], ('id', 'name', 'age'))
# 使用udf
df.select(slen("name").alias("slen(name)"), to_upper("name"), add_one("age")).show()
# 增加一列
df2 = df.withColumn("ont_age", add_one("age"))
print(df2.head(2))
输出结果为:
| slen(name) | to_upper(name) | add_one(age) |
|---|---|---|
| null | null | 22 |
| 4 | LUCY | 21 |
有时候仅仅对DataFrame中的一列进行操作不能满足需求,udf需要有多个参数,这种情况也是可以处理的。 比如说我们做文本分类时通常会使用tf-idf作为特征,在计算idf时,就需要把文档总数和某个词出现的文档数传入到udf中。
from math import log
from pyspark.sql.types import FloatType
from pyspark.sql.functions import lit
def idf(D, Ti):
"""
idf_i = log(D/Ti)
:param D: 文档总数
:param Ti: 包含词t_i 的文档数
:return:
"""
if Ti == 0:
return 0.0
return log(D *1.0 / Ti)
# 把idf注册为一个udf,返回值类型为float
compute_idf = udf(idf, FloatType())
# 文档数
document_count = 40
dataframe = spark.createDataFrame([("hello", 30), ("word", 10), ("example",15)], ("word", "num_count"))
# 需要使用 pyspark.sql.functions.lit 把 document_count 转为字面值,
idf = dataframe.withColumn("idf", compute_idf(lit(document_count), "num_count"))
print(idf.head(2))
输出结果:
[Row(word=u’hello’, num_count=30, idf=0.28768208622932434), Row(word=u’word’, num_count=10, idf=1.3862943649291992)]
如果直接传入document_count到 计算idf的udf中的话,会引起method col([class java.lang.Integer]) does not exist 的错误。主要是因为PySpark把传入的参数都当做一列来处理,而我们的DataFrame中是不存在40这一列的。
idf = dataframe.withColumn("idf", compute_idf(document_count, "num_count"))
Py4JErrorTraceback (most recent call last)
<ipython-input-9-281e0b407efe> in <module>()
...
Py4JError: An error occurred while calling z:org.apache.spark.sql.functions.col. Trace:
py4j.Py4JException: Method col([class java.lang.Integer]) does not exist
at py4j.reflection.ReflectionEngine.getMethod(ReflectionEngine.java:318)
at py4j.reflection.ReflectionEngine.getMethod(ReflectionEngine.java:339)
at py4j.Gateway.invoke(Gateway.java:274)
at py4j.commands.AbstractCommand.invokeMethod(AbstractCommand.java:132)
at py4j.commands.CallCommand.execute(CallCommand.java:79)
at py4j.GatewayConnection.run(GatewayConnection.java:214)
at java.lang.Thread.run(Thread.java:745)
也可以通过lit先把document_count这个字面值添加到DataFrame中成为新的一列,再使用udf计算idf。
new_dataframe = dataframe.withColumn("document_count", lit(document_count))
idf = new_dataframe.withColumn("idf", compute_idf("document_count", "num_count"))
print(idf.head(2))
输出结果: [Row(word=u’hello’, num_count=30, document_count=40, idf=0.28768208622932434), Row(word=u’word’, num_count=10, document_count=40, idf=1.3862943649291992)]
DataFrame中多了两列document_count 和 idf。
阅读全文 »
过拟合危害
2017-12-17
上一篇文章在讲述非线性转换的时候,提到了当非线性转换的次数很高的时候会使$E_{in}$很小,而$E_{out}$很大,并且把这种现象称为过拟合。这篇文章就来具体讲讲什么过拟合,过拟合是怎么产生的,如何处理过拟合。
什么是过拟合
先来看一个例子,现在要做一个一维的线性回归,有5个数据点,这5个数据点是一个二次函数$f(x)=3x^2+2$加上一些噪声产生的。然后用一个4次多项式去拟合这些数据。按照上一篇文章中的步骤,这里用python实现拟合的过程。
import numpy
import matplotlib.pyplot as plt
import random
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
N = 10
x = numpy.array(numpy.arange(-1, 1, 0.2))
y = numpy.array([3*(i **2)+2 for i in x])
noise = numpy.array([random.uniform(-0.1,0.1) for i in range(N)])
Y = y + noise
c = numpy.ones(N)
# 用4次多项式进行非线性转换
X = np.c_[c,x, numpy.power(x, 2), numpy.power(x,3), numpy.power(x, 4)]
# 训练模型
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.5)
model = LinearRegression()
model.fit(x_train, y_train)
#画图
test = numpy.arange(-1, 1, 0.01)
plt.plot(test,3*numpy.power(test, 2)+2 )
plt.scatter(x_train[:,1], y_train, marker='o', color="black")
X_test = np.c_[numpy.ones(test.shape[0]),test, numpy.power(test, 2), numpy.power(test,3), numpy.power(test, 4)]
plt.plot(test, model.predict(X_test), color="red")
拟合的结果如下图所示:
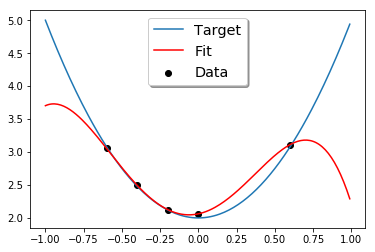
由于训练数据只有5个数据点,而我们用一个4次的函数去拟合,肯定能过得到一条曲线,完美的拟合这5个数据点,即$E_{in}=0$,然而从图中,我们可以看到,拟合出的曲线和我们的目标函数很大的差别,即$E_{out}$很大,这个模型的泛化能力很差。实际上,$E_{in}$、$E_{out}$和VC维的关系就像下面的图像表示的那样,随着VC维越来越高,$E_{in}$越来越小,越来越接近于0,而$E_{out}$却越来越大。
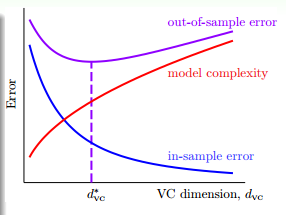
VC维从小到大的过程中,如果$E_{in}$越来越小,但$E_{out}$越来越大,这时就发生了过拟合(overfitting)。反过来,欠拟合就是指,VC维从大到小的过程中,$E_{in}$变大了,$E_{out}$也变大了,这说明模型不能很好地拟合数据。通常来说,欠拟合的情况很好解决,只有增加VC维就好了,但过拟合是一个比较难以解决的问题。
过拟合是怎么产生的
过拟合的一个原因是,使用了过大的VC维,这就像开车开太快会比较容易发生车祸一样;另一个原因是数据集有噪声,这就像是差的路况也会增加出车祸的概率;第三个原因是数据集的数量有限,这就像是去到一个陌生的地方,对路况了解不多,也比较容易出事故。那么噪声和数据集的数量会对过拟合产生什么样的影响呢?
依然是一维的回归分析,我们产生两个数据集:
- 目标函数是一个10次的多项式,数据集用这个目标函数产生,并加上一些噪声。
- 目标函数是一个50次的多项式,数据集用这个目标函数产生。
然后分别用二次多项式($g_2\in H_2$)和10次多项式($g_{10}\in H_{10}$)来拟合这两个数据集。
当使用二次多项式和十次多项式分别拟合10次的目标函数时,E_{in}和E_{out}分别如下表所示:
| 二次多项式 | 十次多项式 | |
|---|---|---|
| E_in | 0.060 | 0.034 |
| E_out | 0.127 | 9.00 |
从二次多项式到十次多项式的时候发生了过拟合。
当使用二次多项式和十次多项式分别拟合50次的目标函数时,E_{in}和E_{out}分别如下表所示:
| 二次多项式 | 十次多项式 | |
|---|---|---|
| E_in | 0.0029 | 0.00001 |
| E_out | 0.120 | 7680 |
使用十次多现实拟合的时候,$E_{in}$非常小,但$E_{out}$却非常大。从二次多项式到十次多项式的时候发生了过拟合。
虽然在做拟合之前,我们已经知道了目标函数分别是10次和50次多项式,然而还是$H_2$的模型取得了比较小的$E_{out}$。这代表了机器学习中的一个哲学:以退为进。虽然简单的模型$E_{in}$比较大,但$E_{out}$却比较接近$E_{in}$。像下图中的学习曲线显示的那样,当数据集有限时,$E_{in}$会比期望的误差好一点,而$E_{out}$会比期望的误差坏一点。而如果是十次多项式的假设空间时,当N无穷大时,$E_{in}$和$E_{out}$也会接近于期望误差,而当N很小时,$E_{out}$却非常大。因此,当N很小时,使用简单的模型(VC维低)虽然不是十分完美,但却能得到一个比较好的结果。
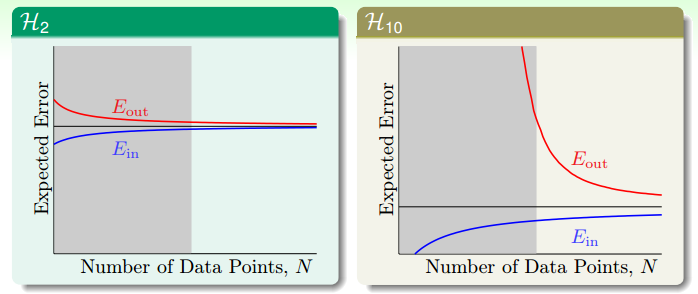
拟合没有噪声的50次的数据样本时,虽然没有噪声,依然是2次多项式的拟合函数取得了较好的结果。因为有限的数据点不足与解释复杂的目标函数。
什么时候会发生过拟合
接下来用一个更细致的实验说明什么时候要小心过拟合的发生。把我们的数据集($y=f(x)+\varepsilon$)分为两个部分,一个是目标函数$f(x)$,另一部分是噪声$\varepsilon$。
- 对数据集加一个强度为$\sigma^2$的高斯噪声,研究不同强度的噪声会对模型产生什么影响。
- 数据集在$f(x)$是一个复杂度为$Q_f$次的函数上均匀分布。
- 数据集的数量N
我们来研究这三个变量变化时,对过拟合产生的影响。
依然用二次多项式$H_2$和十次多项式$h_{10}$对数据集进行拟合。由于十次多项式的模型能力更强,它的$E_{in}$肯定要比二次多项式模型的要小。那么我们就用$E_out(g_{10}) - E_{out}(g_2)$来度量过拟合发生的程度。当两者的差别很大时,过拟合的情况肯定很严重。
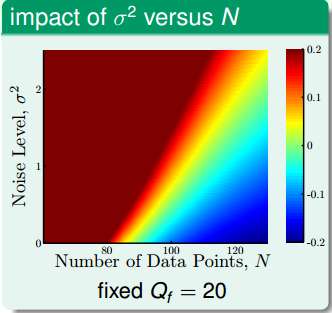
上面这幅图的横轴是数据集的数量,纵轴是高斯噪声的强度$\sigma^2$,目标函数的复杂度固定在20次,图中的颜色代表过拟合的程度。颜色越红,过拟合的程度越高,颜色越蓝,过拟合的程度越轻。从图中可以看到,红色的区域集中在左上角,即当噪声很高,数据集很少的时候,蓝色区域集中在右下角,当数据集很多,而且资料很少的时候。
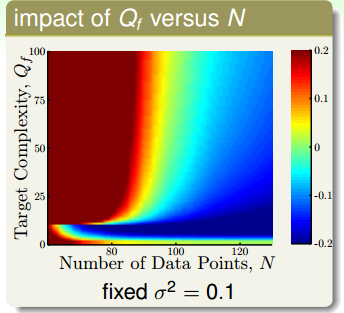
上面的这幅图,横轴依然是数据集的数量,纵轴是目标函数的复杂度,而高斯噪声的强度固定为1。跟上一幅图类似,目标函数的复杂度越高,数据集数量越少,越容易过拟合。值得注意的是,这这幅图的最下方,也有一个区域发生了过拟合。这是因为,当目标函数很简单是,用过于复杂、表达能力过强的模型($H_{10}$)也会发生过拟合的现象。这说明,复杂的模型往往做不好简单的题目。
从上面两幅图发现,我们加上去的高斯噪声会对过拟合产生很大的影响,我们把加上去的高斯噪声叫做随机噪声(stochastic noise)。第二幅图表面目标函数的复杂度也会对过拟合产生很大的影响,我们把这个叫做固定噪声(deterministic noise)。也就是说模型的复杂度跟高斯噪声一样,对过拟合都产生了类似于噪声的效果,差别在于一个是固定的,一个是随机产生的。从这两个图我们可以总结出4个可能会发生过拟合的地方:
- 数据集数量太少
- 随机噪声太强
- 固定噪声太大(目标函数很复杂)
- 模型太复杂(VC维过高)
如何避免过拟合
- 从简单的模型开始
- 数据清理(data cleaning/pruning)
- data hinting,对现有数据的了解,去产生更多的数据
- 正则化
- 验证(validation)
这里先简单说一下data cleaning, pruning 和 hinting,至于正则化和验证会在以后的文章里讲。
数据清理即删除异常点。比如一个数据集被标记为0,但却和标记为1的数据集聚在一起,就可以把这个数据的标记改为1(cleaning),或者直接丢掉(pruning)。数据清理说起来很简单,但困难的地方在于如何侦测哪些数据点是异常点。数据清理的方法可能会有用,但并不是时时都有用。比如分类时,正例和负例都非常多,那偶尔有一个异常点也不会对模型造成很大的影响。但在有些例子里面会产生较大的影响。
在手写字体识别的例子中,假如我们收集到的数据集比较少,我们可以把现有的数据集稍稍的做一下平移和旋转,他们仍然代表同样的数字,这样可以增加样本量。这样用我们造出来的虚拟样本(virtual examples),加入数据集的做法就是 data hinting。这有可能会有用,但要非常小心。因为此时的训练集的分布已经和原始数据集分布不一样了。所以一定要根据学习任务的特征和数据集特点去小心的产生虚拟样本。
阅读全文 »
非线性转换
2017-12-14
二次空间假设
在讲非线性转换之前,我们先回顾一下线性空间假设。
- 从视觉上来看,分割平面是线状的(对于多维空间是超平面)
- 从数学上来看,得分函数是线性的,$s=w^Tx$
- 从统计学上来看,$d_{vc}$(VC维)是有限的,即训练误差$E_{in}$和测试误差$E_{out}$是有限的。
但线性空间假设只对线性可分的数据有效,对于某些线性不可分的数据,不论假设空间中什么样的直线(超平面)都会有很大的$E_{in}$。那么怎么去突破线性模型的限制呢?
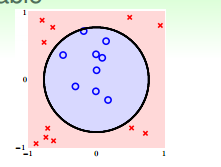
对于像上图这样的样本$D$来说,我们无法用一条直线正确地把数据集分类两类,但可以用一个圆心在原点,半径为$\sqrt{0.6}$的圆把所有的样本正确的分类。此时的假设为:
那么我们是否把之前学过的PLA、逻辑回归、线性回归等算法应用到圆圈可分的数据集上呢?
看下上面的假设$h_{sep}(x)$,分别令
常数项为$z_0$, 每一项对应的系数为$\tilde{w_0}\space\tilde{w_1}\space\tilde{w_2}$, 则圆圈可分的假设空间为:
看到这个式子,是不是很熟悉,这就是线性模型的灵魂,评价函数的形式。
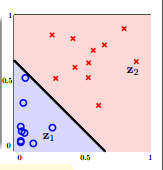
其实这个式子所做的事情就是把原来X空间里面的点都转化到Z空间里面,即把X空间中的每一个点的两个分量分别平方之后,转换到Z空间中,即${(x_n, y_n)} \rightarrow{(Z_n, y_n)}$。数据就变成了线性可分的(如上图所示)。
我们把这样的转换叫做特征转换(feature transform) $\phi$:
经过了一番转换,我们可以在Z空间中找到一条直线把数据给正确的分成两类。
X空间中的数据是圆圈可分的,经过特征转换到Z空间中一定是线性可分的。那么反过来,在Z空间中是线性可分的,是不是说明X空间中的数据肯定是圆圈可分的呢?我们来看一下上面的特征转换$(z_0, z_1, z_2) = Z = \phi(x) = (1, x_1^2, x_2^2)$。 在Z空间中的假设空间为:
这个假设空间中的假设和$tilde{w}=(\tilde{w_0},\tilde{w_1},\tilde{w_2})$的取值有关,我们来看一下当$\tilde{w}$取不同值时,X空间中曲线的形状。
- (0.6, -1, -1): 圆(圆内的样本是圈圈)
- (-0.6, 1, 1): 圆(圆外的样本是圈圈)
- (0.6, -1, -2): 椭圆
- (0.6, -1, +2): 双曲线
- (0.6, +1, +2): 所有的样本都是圈圈
由此可见,Z空间中的直线对应了X空间中不同的二次曲线,对于这个转换来说,这些二次曲线是有限制的,即对称点都在原点,是一些特殊的曲线。那么如何对于到所有可能的二次出现呢?那我们需要把表示二次出现所有的项都包含进来,即:
可以把X空间中所有的二次曲线转换到X空间中,此时的假设空间为:
现在我们可以把圆、椭圆、双曲线、旋转过的椭圆等二次曲线都转换到Z空间。直线和常数作为二次曲线的特例,也可以被转换到Z空间。那么接下来的问题就是如何学习一个好的二次假设g了。
好的二次假设
在上一部分,我们说X空间中的的二次曲线,都可以映射到Z空间中的直线,Z空间中的直线也对应了X空间中的二次曲线。如果我们想要在X空间中找到一个好的二次曲线假设,我们只要在X空间中找到一个好的直线假设,就可以反过来映射到X空间中。
既然我们可以用X空间中的数据集${(x_n,y_n)}$,使用PLA,逻辑回归等方法,找到一个很好的假设,那么对于Z空间中的数据${Z_n=\phi_2(x_n), y_n}$,我们当然可以利用上述算法找到一个好的直线。简单来说,整个步骤如下:
- 首先用转换函数$\phi$把原始数据${(x_n,y_n)}$转换到Z空间${Z_n=\phi_2(x_n), y_n}$。
- 利用数据集${(z_n,y_n)}$,和自己喜欢的线性分类算法$A$去学习一个好的$\tilde{w}$。
- 返回$g(x)=sign(\tilde{w}^T\phi(x))$
上述步骤中,特征转换函数$\phi$和学习算法$A$都是有多种方案可以选择的。如学习算法、可以选择PLA、逻辑回归或者其他分类算法,同样地,特征转换函数可以是三次、四次直到n次。
特征转换的代价
如果一个数据集有d个特征,即$X\in R^d$,经过二次转换函数$\phi_2(x)$转后之后的$z=\phi_2(x)$有多少个维度呢?
转换之后,首先由1个常数项,d个一次项,d个$x_i^2$项,还有$C_d^2$个$x_ix_j$项,加起来总共有$\frac{1}{2}d^2+\frac{3}{2}d+1$项。由此可见经过二次转后后的特征比X空间中多了很多维。那么推广到Q次的多项式转换会增加多少维特征呢?
可以算一下,对Q次的转换,转换之后的维度为:
也就是说要花$O(Q^d)$的时间和空间来计算$z=\phi_Q(x)$和$\tilde{w}$。所以说当Q越大的时候,计算的复杂度越大。
除了计算复杂度增加了之外,自由参数的数量也从X空间的$1+d$个增加到了Z空间的$1+\tilde{d}$个,VC维增加到了$1+\tilde{d}$,这可能会引起过拟合的问题。

像上面的这个图,同样的数据集,左边是用线性分类找出的一个直线分割面,右边是用一个4次曲线转换之后找到的分隔曲线。虽然直线的分割面把训练集的一些点分错了,但那些点离自己正确的类别非常远,有理由认为这些点是噪声点,$E_{out}$和$E_{in}$很接近。而右边的曲线分割面,虽然把所有训练样本的点都分正确了,$E_{in}$是0,但实际情况中,$E_{out}$可能非常大,即泛化能力很差。
所以做非线性转换并不是没有代价的,首先它带来计算和存储上的复杂度,其次有可能导致过拟合的问题。因此,要不要做非线性转换,如何做非线性转换就是一个值得考虑的问题。
那么怎样挑选一个合适的非线性转换次数。对与二维或者三维的数据,我们可能会想把数据可视化,看看数据的分布,然后来挑选一个合适的Q。但如果是4维、5维甚至上百维的数据呢,我们没法形象的把数据可视化出来。此时应该怎么办呢?
结构化的假设空间
我们先定义0维的变换为:
那么一维的变换就是常数再加上所有的一次式:
二次变换为一次变换加上所有的二次式:
三次变换为:
以此类推,Q次的变换为:
即,高次的变换包含了低次的变换,低次的变换是高次变换的特例,这样的假设空间结构是嵌套的。
它们的VC维也符合下面的不等式:
那么它们的$E_{in}$也符合下面的关系:
像下图展示的那样:
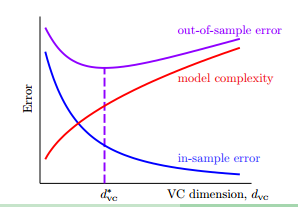
随着VC维的增加,$E_{in}$越来越小,但模型复杂度越来越高和$E_{out}$也越来越大。假如一个初学了非线性变换的人,用100多次的变换跑出来一个模型,做到了$E_{in}=0$,很高兴的想,你看我的模型很厉害,误差是0了呢。但这时候其实是很危险的,因为很可能模型是过拟合了,$E_{out}$很可能是非常大的。那么安全的做法是先从一维的变换,即线性分类开始,如果能够得到一个不错的$E_{in}$,我们就可以很开心的停止模型的训练了。如果$E_in$很大,不满足我们的需求,我们才考虑用更高次的变换。
阅读全文 »
逻辑回归
2017-12-10
逻辑回归的问题
在线性回归这篇文章中,讨论了使用线性模型进行回归学习。PLA(perectron learing althro,感知机学习算法)是一个进行分类任务的线性模型。那如果现在我接到了老板的一个任务,除了能预测出这个用户明天会不会流失之外,我还要告诉我他有多大的可能性会流失,这个时候该怎么办? 此时,我们的预测目标是:
即,要预测出一个0到1之间的值,表示概率值。
我一看预测目标是0到1之间,是个连续的实数,是个回归任务嘛,如果我能有一批用户数据,每个用户数据都有对应的流失概率,我用线性回归去做一下预测,计算一下$w_{LIN}$就好了嘛,这有什么难的。 我想像中的数据:
然后我去数据库中提取数据,然后我傻眼了,以往的数据中,只有一个客户流失了还是没流失,谁会告诉我流失的概率是多大啊。实际我能有的数据只能是这样的:
那现在问题来了,怎样用二分类的样本,在假设空间H中找到一个优秀的假设g,然后用这个g去计算老板需要的概率呢?回归一下上一篇文章里的线性回归和使用线性回归分类:线性回归$y=w^TX$得到了一个实数值,把符号函数$sign$应用到这个实数值上把输出值变为-1和1,就可以用来分类了。那么如果能有一个函数把$w^TX$映射到0到1之间,这样不是可以解决概率的问题吗。那么有这样的一个函数吗?答案当然是有了。他就是logistic function,也叫对数几率函数。
logistic 函数的图像如下所示:
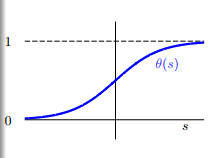
从函数的图像可以看出,logistic函数是一个单调递增的、连续的sigmoid函数。
而且logistic函数还有一个很好的性质,对称性。这条性质在后面会有很大的用处。
现在我用logistic函数把$w^TX$转换为概率,logistic的假设空间就变成了:
误差函数
我们要在假设空间中找到一个最优的函数g去近似理想的函数f(x)。从线性回归那里,我得到一个经验就是,如果要找到一个最优的函数,那我得先找到假设的函数g和理想函数f(x)之间误差的表示方式,然后把误差最小化,误差最小时的那个假设函数就是我要找到最优假设g。
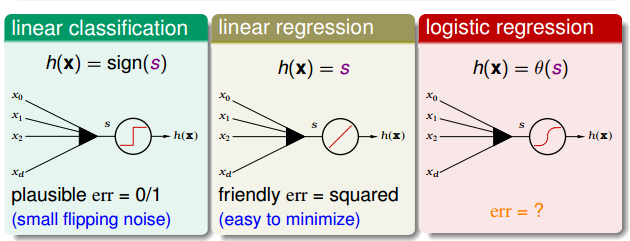
由前一篇文章我们知道,线性模型的打分函数是$s=w^TX$。当线性分类时,误差函数为0/1误差,当线性回归时为均方误差,那么逻辑回归时,误差函数该怎么定义呢?
看一下我们的目标函数 $f(x)=p(+1|x)$,是x是正例时的概率,那么x是负例的概率就是$1-f(x)$, 等价于:
那么我们考虑这样的一个样本集$D={(x_1, \circ), (x_2, \times), …, (x_N, \times)}$:
根据贝叶斯定理,可以推测出数据集D由f产生的概率为:
把上式中的$p(y|x)$换成f(x)可以得到:
由于f是理想的情况,是无法直接得到的,但可以通过学习得到一个假设h,因此可以根据假设h计算生成同样一个数据集的概率,这样的概率称为依然概率:
由logsitic函数的对称性:
如果假设h很接近于理想f,即$h\approx f$,那么h产生数据集D的概率应该很接近于f产生D的概率。而我们既然观察到了数据集D,说明f产生D的概率很大,所以:
因此,可以因为假设空间H中最优秀的那个g应该是似然概率最大的那个,即:
而:
逻辑回归的目的就是找到一个h,使得上式最大化。由于每个h都和一个w关联,因此把w带入h的定义,上式可以写为:
根据对数函数的性质$log(a+b)=log\space a+log\space b$、$log\space (\frac{1}{a}) = -log\space a$且对一个函数取对数不会改变这个函数的单调性,我们可以对上面的式子取对数,使得连乘变成连加:
记$err(w,x_n,y_n) = ln(1+exp(-y_nw^Tx_n))$为交叉熵误差函数,那么$\frac{1}{N}\sum_{n=1}^{N}ln(1+exp(-y_nw^Tx_n))$就是逻辑回归的训练误差$E_{in}$。 即:
逻辑回归中的梯度
有了误差函数,剩下的问题就是怎么求最优的w的问题。经过分析发现,交叉熵误差函数也是一个连续的、二次可微的凸函数,我们仍然可以通过求梯度,让梯度等于0来求$E_{in}$的最小值。即$\nabla E_{in}(w)=0$。 对$E_{in}(w)$进行求导:
因此$E_{in}$的梯度用向量的形式可以表示为:
接下来试着求解$\nabla E_{in}(w)=0$。 注意一下上面的式子,梯度是一个带权的求和,权值是$\theta$。既然梯度是一个加权求和,那么当所有的权值,即$\theta$都是0的时候,就可以使得梯度等于0。那么梯度在什么时候等于0呢,根据$\theta$的定义,即logistic函数的性质,我们知道只有当$y_nw^Tx_n»0$(趋向于无穷大)时,$\theta$才等于0。这就是说$y_n$ 和 $w^Tx_n$要同号,也就是说我们的数据集D是线性可分的。但是梯度是一个加权求和,并不是一个$w$的线性方程,并不能像线性回归那样求得一个解析解。
那么怎么求解最优的w呢,这里介绍一种迭代优化方法,即梯度下降。
梯度下降
迭代优化方法的思想可以表示如下: 对 $t = 0, 1, …$
这里,$v$代表更新方向,$\eta$代表步长。当算法终止时,将得到一个w,这个w就对应了最优的g。
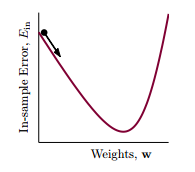
对于向逻辑回归这样的非线性误差函数,当给定了$\eta>0$,我们需要找到一个方向$v$,去一步步的减少误差,就像一个处在山顶的小球,要沿着一个方向滚下山。为了简单起见,先假设每一步都走单位长度,误差函数为
但此时的误差函数仍然是一个非线性的函数,而且加了$|v|=1$的限制,并不比求解$min\space E_{in}(w)$容易。对于任何一条曲线,如果只考虑很小的一段时,都可以近似为一条直线,这样把非线性的函数转成了线性函数,可以降低我们的复杂度。当\eta足够小时,根据泰勒展开有:
在这个式子中,$E_{in}(w_t)$是一个常数,$\eta$是一个给定的大于0的数,\nabla E_{in}(w_t) 可以根据误差函数求出来的,只有$v$是需要我们确定的。数学中学习导数,我们知道,梯度的几何意义就是函数增加最快的方向。具体来说,对于函数$f(x,y)$,在点$(x_0,y_0)$,沿着梯度向量的方向就是$(\partial f/\partial x_0, \partial f/\partial y_0)$的方向是f(x,y)增加最快的地方。那么我们沿着梯度的反方向向下走,就是最快的方向了,最好的$v$就是梯度的反方向,而且我们要求$v$是单位向量,所以有:
把这个v代入到迭代优化的式子中,可以得到$w_t$沿着梯度的方向走一步就得到了$w_{t+1}$:
这个方法通常称为梯度下降。
这时,我们来看一下什么样的$\eta$是不好的方向。
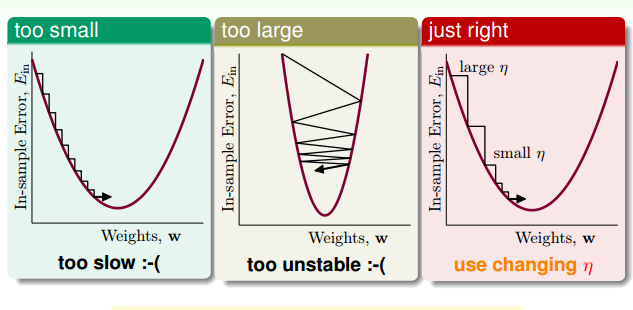
像上面的图一样,如果$\eta$太小,一步走的路程太短,下降的速度很很慢,造成迭代次数增多,下降很慢。而当$\eta$太大时,我们以为是在一条直线上下降,而实际上却有可能跨过最小点,走到对面的山坡,造成震荡的情况。当坡度比较大的时候,我们可以选择稍微大一点的$\eta$,使下降的速度快一点,而当坡度很小的时候,要适当的减小$\eta$,使得跨一步不至于太大,而跨过最小点。因此合适的$\eta$要根据坡度的大小来调整,即:
回头看下$w_{t+1}$的更新式子,分母正是$|\nabla E_{in}(w_t)|$,如果用$\hat{\eta}$ 表示$\frac{\eta}{|\nabla E_{in}(w_t)|}$, 那么$w_{t+1}$更新的式子可以表示为:
由于$\eta$和 $|\nabla E_{in}(w_t)|$ 正相关,那么如果我们可以让$\eta$和 $|\nabla E_{in}(w_t)|$ 成比例,此时,$\hat{\eta}$就是个常数。为了方便,我们把$\hat\eta$上的帽子去掉,仍记做$\eta$,即,$w_{t+1}\leftarrow \eta \nabla E_{in}(w_t)$。通常,我们把$\eta$称为学习率。
所以,逻辑回归的学习算法应该是:
初始化一个$w_0$
对 $t = 0, 1, …$
-
计算
-
更新
直到$\nabla E_{in}(w_{t+1}) \approx 0$ 或者已经迭代了足够多的次数。此时得到的$w_{t+1}$就是最优的假设。
阅读全文 »
is和==的区别
2017-12-05
is 和 == 的区别
我们先来看一段代码
>>> a = 1
>>> b = 1
>>> a == b
True
>>> a is b
True
>>> c = 1000
>>> d = 1000
>>> c == d
True
>>> c is d
False
会不会觉得很奇怪,在上面的代码中 a==b, c==d 的值都是True,这在我们的预料之中,
那为啥a is b 和 c is d 这两个表达式的值不同呢?
要回答这个问题,我们首先来看一下Python的数据模型(data model)。
数据模型
在Python中,一切都是对象,即使是内建类型和函数也是对象。每一个对象有一个标识符(identity),
一个类型(type)和一个值(value)。
对象的identity一旦被建立,就不会被改变了,现阶段(Python2)可以认为identity 就是这个对象在内存中的地址。
Python的内建函数id()返回一个整数代表对象的identity(现阶段id()的实现就是对象的地址)。
一个对象的type也是不可改变的。type决定了对象支持哪些方法,也定义了这个对象可以接受哪些值。
我们可以用内建函数type()返回一个对象的type。
有些对象的值是可以改变的,这些对象称之为mutable,比如dict,list等;有些对象的值是不可变的,这些对象称之为immutable,
比如str,int, tuple等。
is 和 == 比较的是啥?
了解了Python的数据模型,现在我们可以来说说,is和==比较的是啥了。
==
python2 的官方文档上有说明,操作符 <, >, ==, >=, <=, and != 比较两个对象的值。
比较的对象必须是同一种类型。如果两个对象不是同一种类型,那比较结果总是不想等的。
相同类型的对象之间的比较行为取决于对象的type:
- 数字(Numbers)就是数学意义上的比较。
- 字符串(Strings): 先用内建函数
ord()计算出每个字符的数字结果,然后再进行比较。 对于ascii表中的字符,str和unicode能得出一样的结果,如:>>> 'abc' == u'abc' True然而对于超出ascii的字符就不一样了,
>>> '中国' == u'中国' False不一样的原因,和编码的问题有关系,这块没有仔细研究过,先不说了。
- 元祖(tuples)和列表(lists)按顺序一一比较内部的元素。如果两个元祖(列表)相等,意味着 元祖(列表)中的每个元素都相等,并且这俩元祖(列表)的长度也想等。
- Mapping(dictionaries), 两个Mapping对象相等,除非他们的sorted(key, value)list 相等。
- 许多其他的内建类型只有是同一个对象的时候才相等。
isis比较的是对象的标识符即identity。 只有a和b是同一个对象的不同引用时,a is b才是True。is not相反。
说到这里,再回头去看开头的代码,a 和 b 的值相等,c 和 d 的值相等,所以 a==b和c==b都是True。
等等,那a 和 b 为啥是同一个对象,c 和 d为啥又不是同一个对象啦? 别急,这里还有一个概念要说。。。
字符串驻留(Stirng Interning)
[String Intering] (https://en.wikipedia.org/wiki/String_interning) 在维基百科上是这样解释的:
In computer science, string interning is a method of storing only one copy of each distinct string value, which must be immutable. Interning strings makes some string processing tasks more time- or space-efficient at the cost of requiring more time when the string is created or interned. The distinct values are stored in a string intern pool.
翻译过来就是说每个不同的字符串只保存一份在字符串驻留池(string intern pool)中,这些字符串都是不可变的。 字符串驻留技术使得字符串在创建或驻留时需要等多的时间或空间。字符串驻留技术能够使字符串的比较工作更快。具体的技术实现和优点 在这里就不多说了啊,大家有兴趣的自己去查资料(其实是我也没看呢)。 很多面向对象的语言,Python,PHP,lua,Java等都实现了字符串驻留。 这样我们就可以明白,当我们写下
>>> s1 = 'abcde'
>>> s2 = 'abcde'
这两行代码时,我们实际上只创建了一个字符串对象,s1 和 s2都是对这个对象的引用,所以s1 is s2的值是True。
>>> s1 is s2
True
但并不是所有的字符串都会被驻留,只有一些简单并常见的字符串才会被驻留,像下面这个随意在键盘上敲出来的字符串,就没有被驻留。
s3和s4是两个不同的对象。
>>> s3 = 'hdkghiddfdlkg;seod'
>>> s4 = 'hdkghiddfdlkg;seod'
>>> s3 is s4
False
>>> s3 == s4
True
除了字符串,其他的对象也可以应用驻留技术。维基百科上有这样一句话:
Objects other than strings can be interned. For example, in Java, when primitive values are boxed into a wrapper object, certain values (any boolean, any byte, any char from 0 to 127, and any short or int between −128 and 127) are interned, and any two boxing conversions of one of these values are guaranteed to result in the same object.
大意是说java的基本类型被包装为相应的对象的同时,会把这个值也保留在驻留池中。对同一个值的两次装箱过程会是同一个对象(是这么说的吗?)。
在Python的文档中也说,对于不可变类型(immutable types)产生新值的操作实际上会返回一个引用,
这个引用会指向一个已经存在的类型(type)和值(value)都和我们的结果一样。因此在开头的代码中a 和 b并不是产生了两个不同的对象,
而是同一对象的两个引用。虽然目前我看到的文档中并没有说明,Python采用的是何种技术,我猜测可能是驻留技术。
对于较小的整数,Python会返回驻留池中对象的一个引用,而对于较大的整数,
不在Python的驻留池中,则直接创建对象。因此,开头的代码中c和d是两个不同的对象,在内存中的地址不一样,c is d当然是False了。
这个结论对于数学计算除来的部分结果也适用:
>>> a = 19
>>> b = 1020-1001
>>> a is b
True
但不是所有的情况都适用:
>>> s1 = '123'
>>> s2 = '123'
>>> s1 is s2
True
>>> s3 = ''.join(['1', '2', '3'])
>>> s1 is s3
False
>>> s1 == s3
True
至于驻留的范围,我还没有找到,如果找到,在更新吧。
说了这么多,还是如果要比较对象是不是同一个对象那就用is, 如果要比较对象值是否相等,那就用==。
阅读全文 »
文本特征的选择
2017-12-05
文本特征选择
文本的特征选择(feature selection)是从训练集所出现的所有词(terms)中选出一个子集,只用这个子集作为文本分类 的特征来训练分类器的过程。为啥要做特征选择呢?一、减少特征空间的维度,加快模型的训练速度和预测速度。 二、去掉对分类没什么帮助的噪声特征,提高分类准确度。下面介绍几种常用的特征选择方法。
基于频率的特征选择方法
基于频率的特征选择方法,顾名思义就是选择某个类别里面出现最多的词作为特征。这里频率可以被定义为文档频率(Document Frequency, DF) 或者collection frequency。DF是指在类别c中包含特征t的文档数,更适用于Bernoulli model。collection frequency 则是指特征t在类别c中出现的次数, 适用于 multinomial model。
基于频率的方法只考虑一个词和在一个类别中出现的频率,因此会倾向于选择一些出现的次数很多但对分类没有什么贡献的通用词, 比如新闻中通常出现的时间、月份等。但当特征选择的够多(几千个)的时候,基于频率的方法也会有不错的表现。这是因为当选择的特征够多的时候, 那些重要的类别指示词也会被选择到特征中。
互信息
互信息(Mutual Information, MI)度量两个事件集合之间的相关性。平均互信息的定义如下
在文本特征选择中,我们可以通过上述公式计算类别c和特征t的互信息,以此来度量一个特征的出现或缺失对做出正确的分类决策的贡献大小。
假设U是一个代表$e_t=1$(包含特征t的文档)和 $e_t=0$
(不包含特征t的文档)的随机变量,C是一个代表$e_c=1$ (属于类别c的文档)
和(不属于类别c的文档)$e_c=0$,那么文本特征选择公式就是:
根据大数定理,我们可以用频率去估计公式中的概率。 另 $N_{**})$表示当$e_t$ 和 $e_c$的值取对应的下标时的文档数。 例如: $N_{10}$表示包含特征t但不属于类别c的文档数;$N_{11}$表示包含特征t且属于类别c的文档数; 以此类推。可以得到$N=N_{10}+N_{11}+N_{01}+N_{00}$,$N_{1.}=N_{10}+N_{11}$ 。 根据大数定理,我们可以估计当U=1,且C=1时的概率,$P(U=1,C=1)=N_{11}/N)$。据此,我们可以把上面的互信息公式重写为:
互信息度量特征t包含了类别c的信息量。如果特征t在类别c中的分布和所有文档中的分布完全相同,那么$IU;C)=0$。如果一个 特征能够完全确定一篇文档的类别,那么它的互信息也会达到最大。 根据上述公式计算出每个特征t和类别c的互信息之后,我们可以把每个特征t的互信息值按照从大到小排序,然后选择前K个特征作为训练模型的特征词汇。
卡方统计
在统计学中,卡方检验通过观察实际值与理论值得偏差来检验两个随机变量是否相互独立。具体的做法是,先假设两个变量 是独立的,即原假设。然后看观察值与理论值直接的偏差程度,如果偏差程度足够小,我们就接受原假设,即两者是相互独立的,误差是由抽样或者测量带来的误差。 如果偏差程度很大,我们就认为两者是相关的,否定原假设。
在特征选择中,两个随机事件分别是特征是否出现$e_t$ 和类别是否出现$e_c$。假如特征t的出现与否,对类别c的判断毫无关系, 我们就可以认为特征t和类别c相互独立,那么此时两者的卡方统计量应该接近于0,而当两者的卡方统计量很大时,则特征t对类别c的 判断会有较大的影响。 我们可以根据下面公式计算$e_t$ 和$e_c$的卡方值,然后排序,选取最大的k的特征作为训练模型的特征空间。
其中N是观察到的频率,E是期望频率。例如$E_{11}$是特征t和类别c同时出现的期望。
同样计算出$E_{00}$、$E_{10}$、$E_{01}$ 和$D_{00}$、$D_{10}$、$D_{01}$带入到卡方公式中, 可以得到
卡方统计的一个缺点是会放大稀有词的显著性。假如有一个词在所有的特征中仅仅出现了2次,这2次都在类别c中,这个词就是统计显著的,但出现次数这么少的词对于分类是没有什么帮助的。
信息增益
信息熵(information entropy)度量样板集合纯度最常用的一个指标。假定当前样本集合D中第k个类别所占的比例为$p_k)(k=1,2,…,|Y|$, 则样本D的信息熵定义为:
Ent(D)的值越小,D的纯度越高。
假如离散的属性a可能的取值为 ${a^1,a^2,…,a^v}$,现在使用a把样本D划分为v个子集,其中第v个子集包含了D中所有在特征a上取值为 $a^v$的样本,记为$D^v$,我们可以根据上面信息熵的定义计算出$D^v$ 的信息熵。再考虑到不同的样本子集包含的样本数不同,给每个子集一个权重$|D^v|/|D|$($|D|$为样本D的个数), 即样本数越多的子集影响越大,可以计算出属性a对样本D的进行划分所得到的信息增益(information gain)
一般而言,信息增益越大,则用a进行划分得到的纯度提升越大。因此,一般情况下,信息增益被用来做决策树的划分属性选择。
在文本特征选择中,特征t只有出现或者不出现{0,1}两种情况。因此,信息增益
此时,信息增益度量的是一个特征t对整个分类的贡献,不能度量对某个类别的贡献。因此,信息增益只能做全局的特征选择, 即所有的类都共用一套特征集合,不能针对某个类别选择本类别特有的特征集合。
上述的特征选择方法各有优缺点,比较多的实验证明卡方统计会有比较好的效果。但具体实验时是不是要做特征选择,选择哪种方法,特征集的大小取多少,还是要靠实验对比来决定。
参考文档:
周志华《机器学习》4.2 划分选择